The definition of availability and how
that availability is measured is one of the key factors in the choice
of technology you will use to implement in your design. One of the
critical factors to establish is how the availability of the system
will be measured and what the context for that measurement will be. We
will use the following formula to calculate availability levels:
percentage availability = (total elapsed time – sum of downtime)/total elapsed timeM
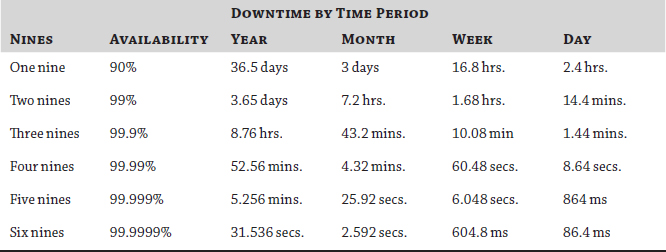
Using the example of 99.9 percent
availability, which is often noted as “three nines” availability, this
translates to the system suffering downtime of 8.76 hours on an annual
basis. That may not sound like a lot; if the measure is changed to
three nines per day, this translates to 1.44 minutes of downtime, which may or may not be enough time for a reboot to occur.
If you calculate the permutations from one
nine to five nines, you will understand why you don't often hear of
systems that are available beyond five nines, as shown in from Table 1. This depends, however, entirely on how the availability is measured.
TABLE 1: Availability by the nines
Defining Availability Components
One of the many things you'll do during
requirement elicitation is to help the business define and understand
the services that Exchange delivers in terms of Exchange availability.
At minimum, Exchange availability is a superset of dependency services.
These services may be classified as follows:
- Client access
- Email transport
- Email storage
For the sake of clarity, we will not
define auxiliary services such as message hygiene third-party
application integration, or the many other examples that come to mind.
Assuming you are satisfied to continue with the three basic services
listed, your criteria may also include that availability could be
measured per service. The availability of a system consisting of
several independent critical components is a product of the
availabilities of each individual component. The product is calculated
by multiplying together the availabilities of each individual component
in the following manner:
A(n) = A1 × A2 × . . . × An
In the case of three components, our equation becomes
Let us examine a hypothetical example of three nines availability across three hypothetical components, as shown in Table 2.
Using Excel, you would list the three availability components and use
the PRODUCT function to multiply the three numbers together. Or, you
could simply multiply the first number by the second number and then by
the third number to obtain the fourth number, or result. Since we have
multiplied three numbers together to obtain a fourth number, we need to
move our decimal to the left by four places, or divide by 10,000 (four zeroes), to obtain a number that may be expressed as a percentage availability. The result will look similar to Table 2.
TABLE 4.2: Component availability
| COMPONENT |
PERCENT AVAILABILITY |
| Client access |
99.9 |
| Email transport |
99.9 |
| Email storage |
99.9 |
| Total availability |
99.7 |
Notice that the total availability is
lower than the availability of any of the component pieces. In order to
build a system with a particular stated resilience, the components'
availability requires examination. This may include network, power,
chassis, and storage availability to name just a few, because these are
all dependent features in larger systems.
Figure 1
illustrates the interdependency of component systems. Note that each
one of the boxes of components can carry its own availability
measurement when calculating total system availability.
FIGURE 1 Interdependent systems Credit: Boris Lokhvitsky
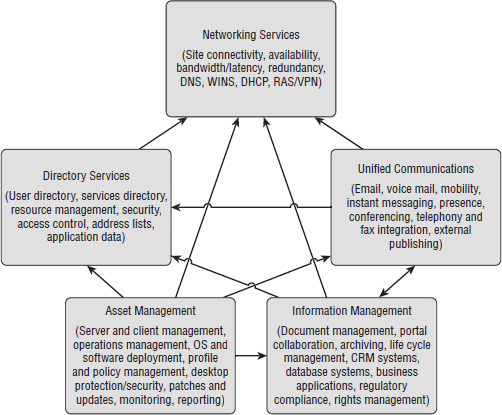
Figure 1
clearly illustrates that it is extremely difficult to establish even
theoretical total system availability when so many systems are
interrelated. When agreeing on the resulting availability of the
desired system, clarify the definition of availability, downtime, and
scheduled downtime as it pertains to the business.
Scheduled system downtime
classically is not included in how availability is measured—in our
three nines example, 1.44 minutes per day does not allow for much
action to be taken. However, if the measure is adjusted to per year,
then 8.76 hours becomes much more plausible for system maintenance.